传感器随机误差与系统误差的区别和联系

传感器随机误差与系统误差的区别和联系

随机误差是许多微小的、独立的、不可分割的系统误差的统计综合。或者说，它是多种因素造成的许多微小误差的总和。

显然，它的产生是由于各种互不相关的独立因素围绕其平均值产生随机起伏。例如，电磁场的变化、环境温度的起伏、空气扰动、大地微震、仪器结构参数的波动、测试人员感觉器官的生理变化等，都对测量结果造成综合影响。正由于上述原因，尽管在测量过程中实验条件没变，并以同样的细心对被测量进行了多次重复观测，只要仪器的灵敏度足够高，就会发现每次所测得的数据，其最后一位或几位的数值不完全一样，这就是由随机误差造成的。

随机误差是许多微小的、独立的、不可分割的系统误差的统计综合。

从数学角度出发，自然界的规律一般可分为函数性质的规律（动力学规律）和统计性质的规律（统计学规律）。例如，牛顿第二定律F=ma，欧姆定律U=IR和系统误差所服从的规律，均属动力学规律。然而，气体对密闭容器壁的压力所遵循的规律却与上述规律不同。无数气体的分子在密闭容器内各按自已的方向和速度杂乱无章地运动着，它们彼此碰撞，并碰击器壁，于是形成压力。初看起来，这种运动毫无规律。但从总体来看，在单位时间内，碰击器壁单位面积上的分子平均次数却是一样的。因此，在器壁上各处都承受着相同的压力。如果增加容器内气体的数量，则在单位时间内，器壁在单位面积上所受到的撞击次数就会增多，于是压力也增大。玻意尔-马略特定律就是用来说明这种客观规律的。但这种规律是大量气体分子所固有的，对单个气体分子没有这种规律性。与此相似，一次测量的单个随机误差没有任何预知的确定规律，但是通过大量的测量实践发现，在多次重复测量的总体上，随机误差却服从统计规律。统计规律中，最基本最重要的一种就是高斯正态分布。服从正态分布的随机误差具 有抵偿性，即随着测量次数n的增多，绝对值相等、符号相反的随机误差，其出现的次数趋于相等，从而导致各次测量误差δ1，δ2，...,δn的总和具有正负抵偿的性质，特别是当测量次数趋于 无穷时，其总体平均值（又称数学期望）趋近于零，即

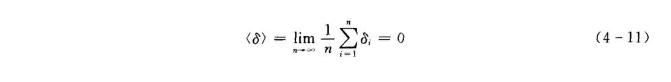
习惯上将这种具有抵偿性的随机误差称作偶然误差。

应当指出，在一定条件下，系统误差和随机误差可以相互转化。对某一具体误差来说，在 某种条件下是系统误差，而在另一条件下可能是随机误差。例如，指示仪表标尺的分度误差， 对制造厂来说，在进行盘点时可能画得偏大些或偏小些，具有随机性质，故为随机误差；而对检定部门来讲，如用该表作为标准表来检定其他仪表时，该表的刻度误差使传递给被检表的数值始终大些或小些，这就转化成系统误差了。再如，电源电压变化引起的误差，如考虑慢变化的平均效应，可视为系统误差；当考虑其瞬时波动时，就应视为随机误差了。因此，在区分误差的性质时，必须注意所指的条件。又如，度盘的某刻度具有一个恒定系统误差，但各刻度的误差大小和符号却不相同。这样，在度盘位置固定的情况下测量定角，则误差恒定；但是如果在均匀改变度盘位置的情况下来测量该角，则误差将时大时小，时正时负，而已随机化了。因此，当掌握了误差的转化条件后，就可将系统误差转化为随机误差，并用统计学的数学方法进行处理，以减小其影响；反之，也可将随机误差转化成系统误差，采用修正的办法进行消除。

总之，在系统误差与随机误差之间并不存在绝对的界限。当某些误差尚未确切掌握其变化规律时，可按随机误差处理。但随着对误差性质认识的深化和测量技术的发展，当这些误差的变化规律一旦被掌握之后，就应把它们从随机误差中分离出来，而按系统误差处理。